新智元报道

编辑：桃子

【新智元导读】Pytorch团队推出的最新3D可视化最新工具mm，能够将矩阵乘法模拟世界还原。

矩阵中的模拟世界，真的来了。

矩阵乘法（matmul），是机器学习中非常重要的运算，特别是在神经网络中扮演着关键角色。

Pytorch团队最新的一篇文章中，介绍了「mm」，一个用于matmuls和matmuls组合的可视化工具。

因为使用了三个空间维度，mm能够有助于建立直觉、激发想法，尤其适合（但不仅限于）视觉/空间思维者。

英伟达高级科学家Jim Fan表示，进入神经网络「矩阵」。

这是一个非常酷的可视化工具，用于矩阵、注意力、并行等等。最好的教育来自最直观的传递。这是一个具有数据并行分割功能的多层感知器。

有了三个维度来组成矩阵乘法，再加上加载训练过权重的能力，就可以用im来可视化像注意力头这样的大型复合表达式，并观察它们的实际表现。

mm工具能够交互，可在浏览器或笔记本notebook iframe中运行，并在URL中保留其完整状态，共享对话链接。

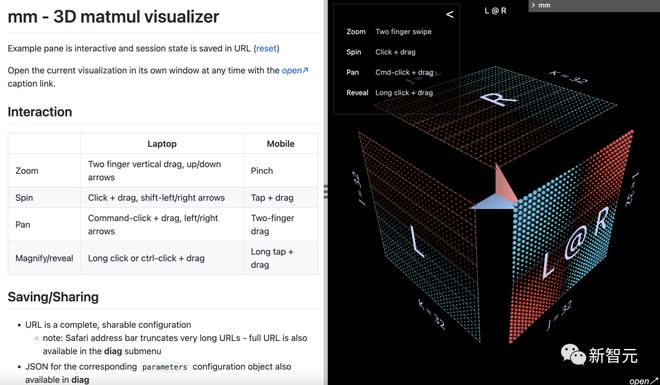
地址：https://bhosmer.github.io/mm/ref.html

下文中，Pytorch提供的参考指南中，介绍了mm所有可用的功能。

研究团队将首先介绍可视化方法，通过可视化一些简单的矩阵乘法、和表达式来建立直觉，然后深入研究一些更多的示例。

为什么这种可视化方式更好？

mm的可视化方法基于这样一个前提，即矩阵乘法从根本上说，是一种三维运算。

换句话说：

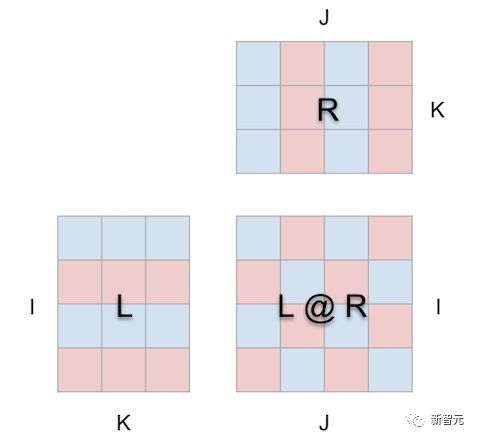
是一张纸，用mm打开后变成如下的样子：

当我们以这种方式，将矩阵乘法包在一个立方体周围时，参数形状、结果形状和共享维度之间的正确关系全部都会建立起来。

现在，计算就有了几何意义：

结果矩阵中的每个位置 i, j 锚定了立方体内部沿深度维度 k 运行的向量，其中从 L 中的第 i 行延伸出水平面和从 R 中的第 j 列延伸的垂直平面相交。沿着这个向量，来自左右2个参数的 (i, k) (k, j) 元素对相遇并相乘，得到的乘积沿着 k 相加，存入在结果的位置 i, j 。

这就是矩阵乘法的直观含义：

- 将两个正交矩阵投影到立方体内部

- 将每个交叉点上的一对数值相乘，形成一个乘积网格

- 沿第三个正交维度求和，得出结果矩阵

为了确定方向，mm工具会在立方体内部显示一个指向结果矩阵的箭头，蓝色指标来自左侧参数，红色指标来自右侧参数。

该工具还会显示白色指引线，以指示每个矩阵的行轴，不过在这张截图中这些指引线很模糊。

对于方向，该工具在多维数据集内部显示一个指向结果矩阵的箭头，蓝色叶片来自左参数，红色叶片来自右参数。该工具还显示白色指南来指示每个矩阵的行轴，尽管它们在这个屏幕截图中很模糊。

当然，布局限制简单明了：

- 左参数和结果必须沿着它们共享的高度 (i) 维度相邻

- 右参数和结果必须沿其共享的宽度 (j) 维度相邻

- 左参数和右参数必须沿着它们共享的（左宽/右高）维度相邻，这就是矩阵乘法的深度 (k) 维度

这个几何图形，为我们提供了可视化所有标准矩阵乘法分解的坚实基础，以及探索矩阵乘法的非难复杂组合的直观依据。

下面，我们就会看到真正的矩阵世界。

规范矩阵乘法分解动作

在深入研究一些更复杂的示例之前，Pytorch团队将介绍一些直觉构建器，以了解事物在这种可视化风格中的外观和感觉。

首先是标准算法。通过对相应的左行和右列进行点乘计算每个结果元素。

我们在动画中看到的是乘法值矢量在立方体内部的扫描，每个矢量都会在相应位置产生一个求和结果。

这里， L 的行块填充为1（蓝色）或-1（红色）；R 的列块填充类似。k 在这里是24，因此结果矩阵（ L @ R ）的蓝色值为24，红色值为-24。

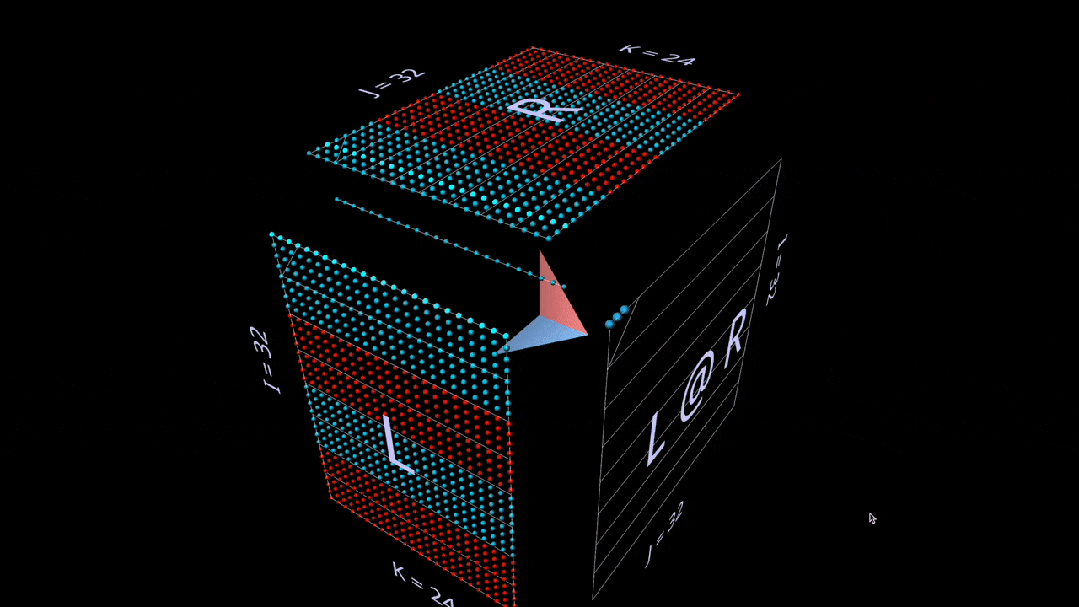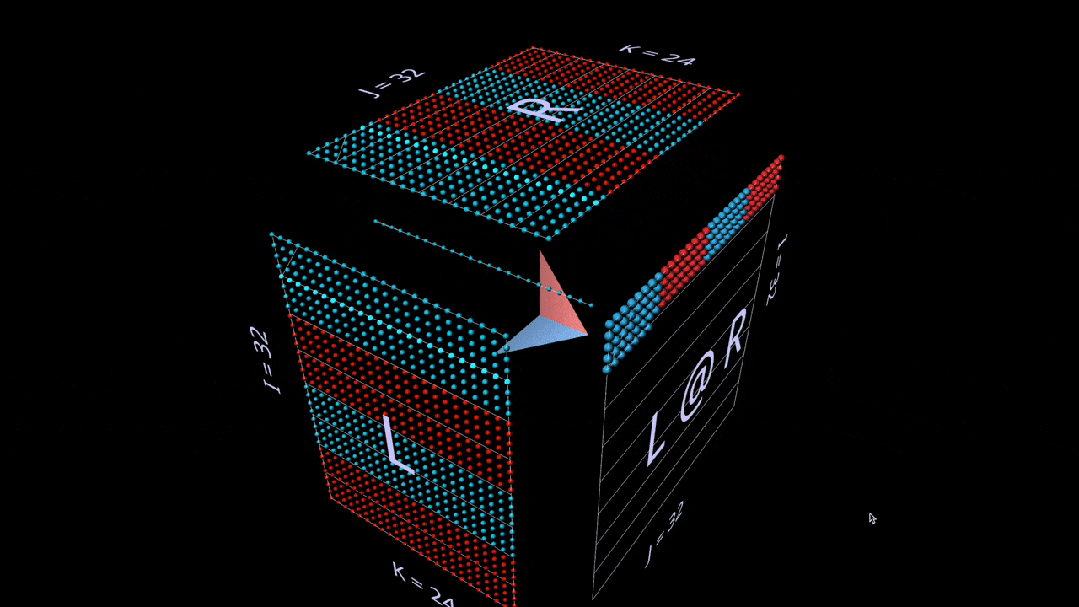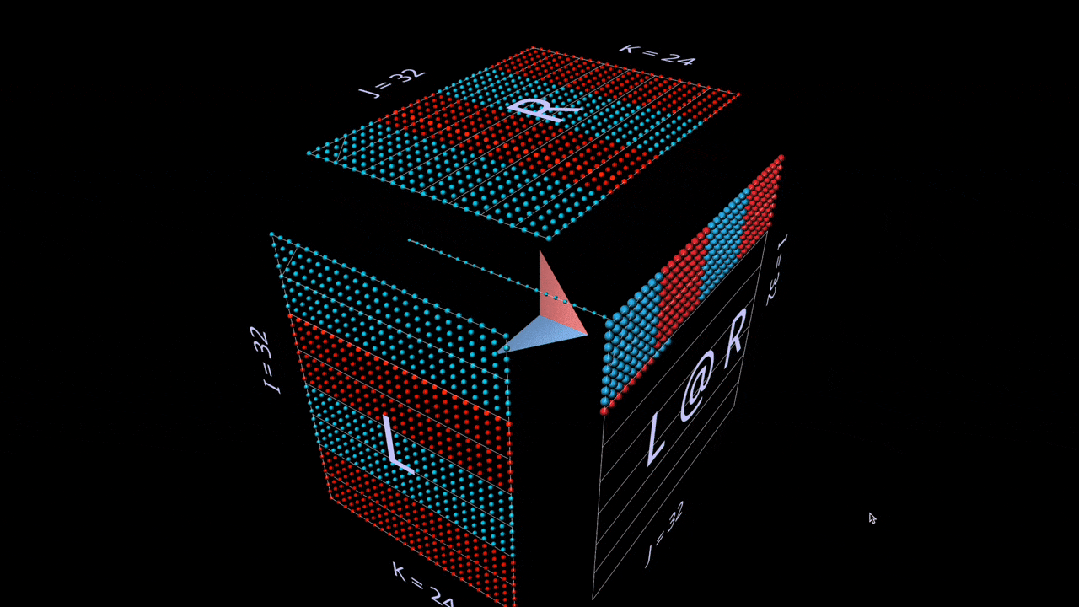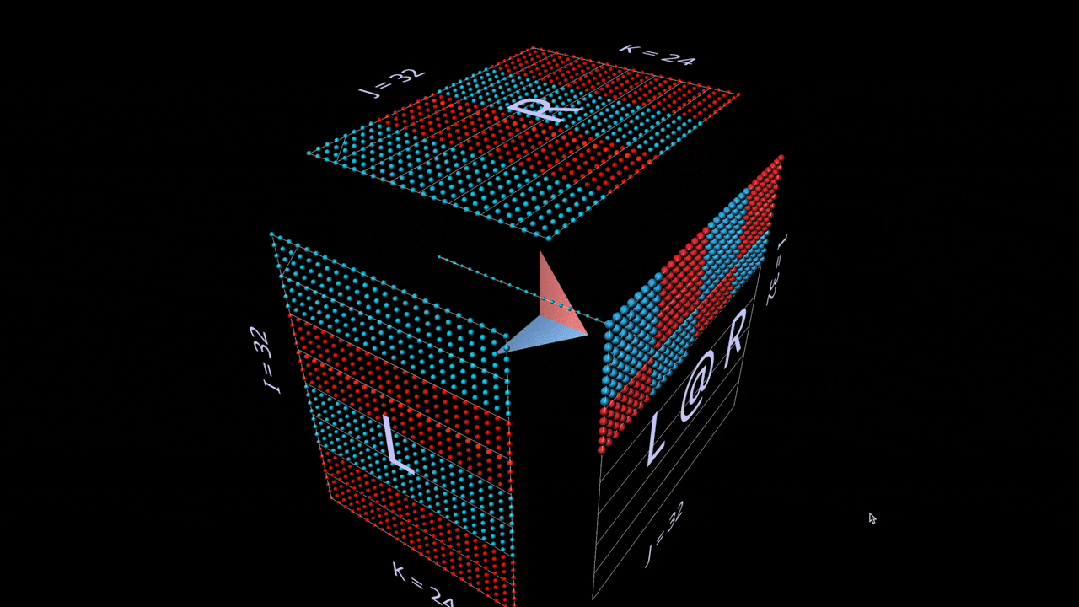
矩阵-向量乘积

分解为矩阵向量乘积的matmul，看起来像一个垂直平面（左参数与右参数每列的乘积），当它水平扫过立方体内部时，将列绘制到结果上。

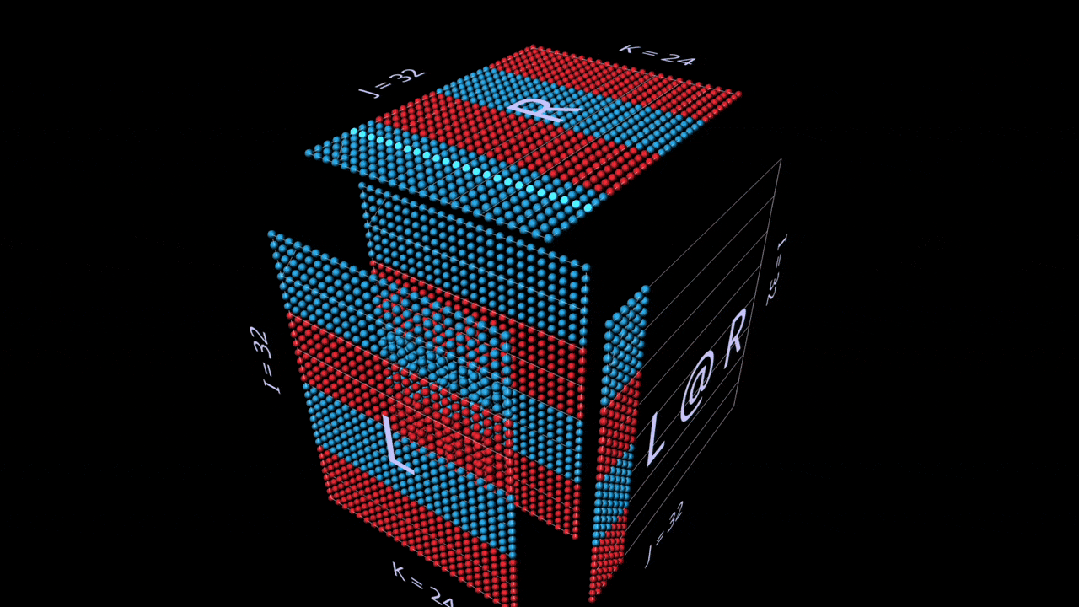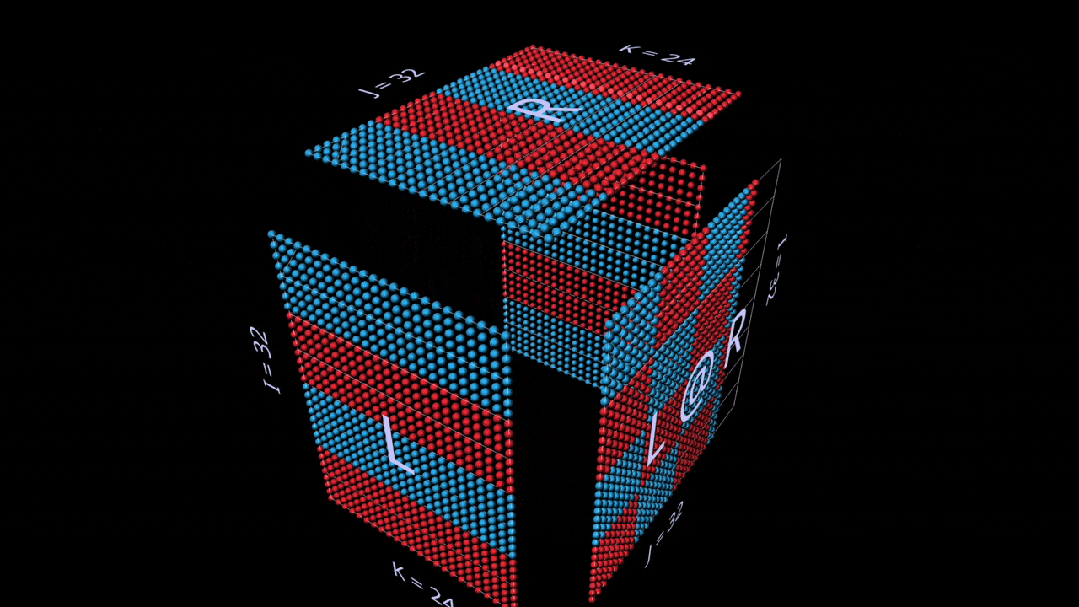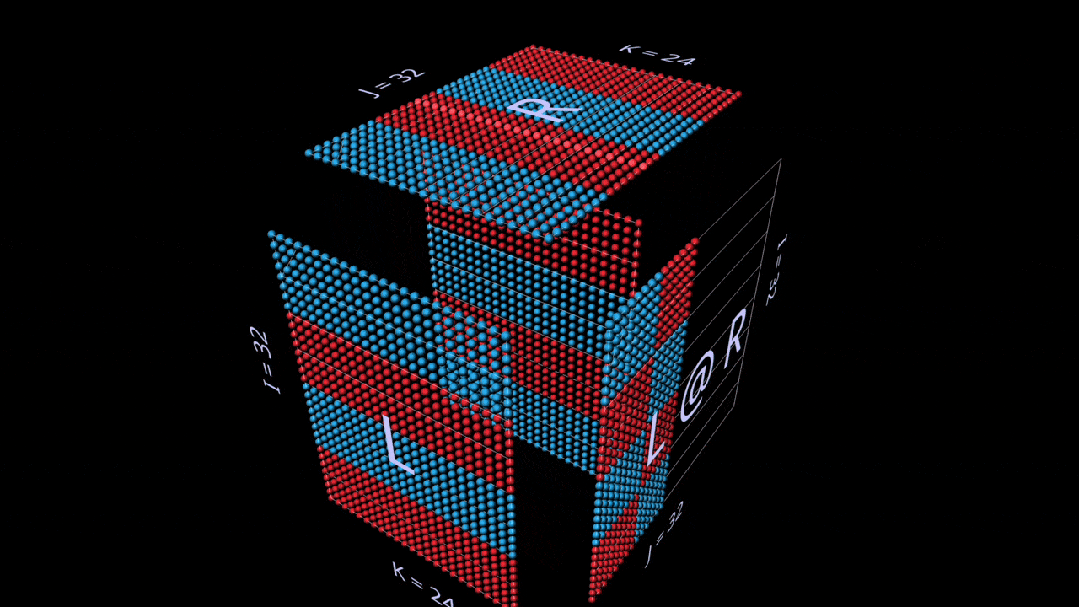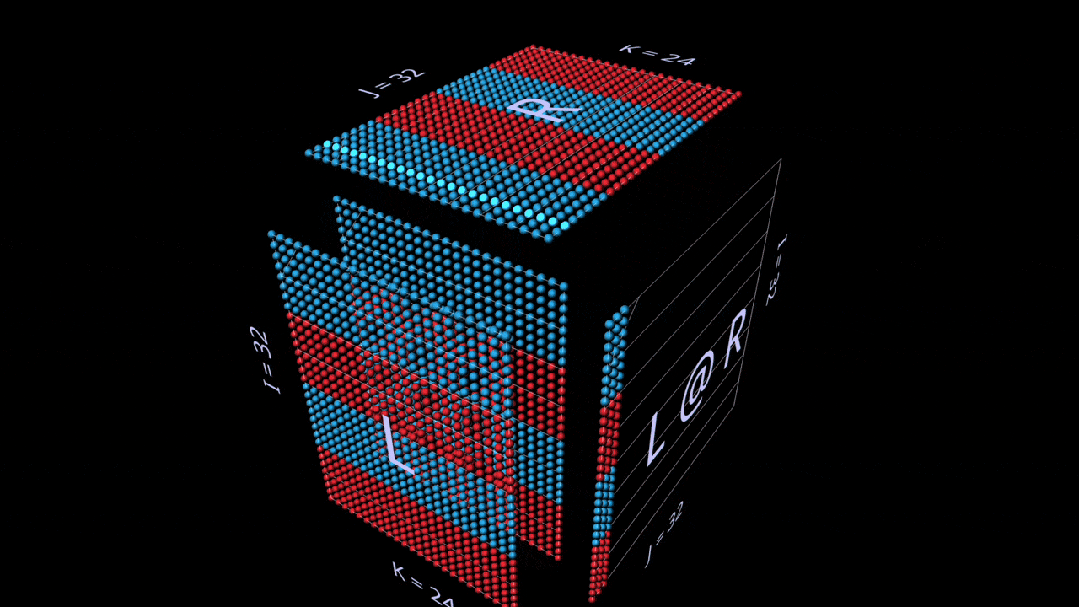
即使在简单的例子中，观察分解的中间值也会非常有趣。

例如，当我们使用随机初始化参数时，请注意中间矩阵-向量乘积中突出的垂直模式。这反映出每个中间值都是左参数的列缩放复制品：

向量-矩阵乘积

分解为向量-矩阵乘积的矩阵乘法在穿过立方体内部时，看起来就像在结果上绘制行的水平面：

切换到随机初始化参数时，我们会看到与矩阵-向量乘积类似的模式，只不过这次的模式是水平的，因为每个中间向量-矩阵乘积都是右参数的行缩放复制品。

在思考矩阵乘法如何表达其参数的秩和结构时，不妨设想一下在计算中同时出现这两种模式的情况：

这里还有一个使用向量矩阵乘积的直觉构建器，显示单位矩阵如何像镜子一样，以45度角设置其反参数和结果：

求和外积

第三个平面分解沿k轴进行，通过向量外积的点和计算出矩阵乘法结果。

在这里，我们看到外积平面「从后向前」扫过立方体，累积成结果：

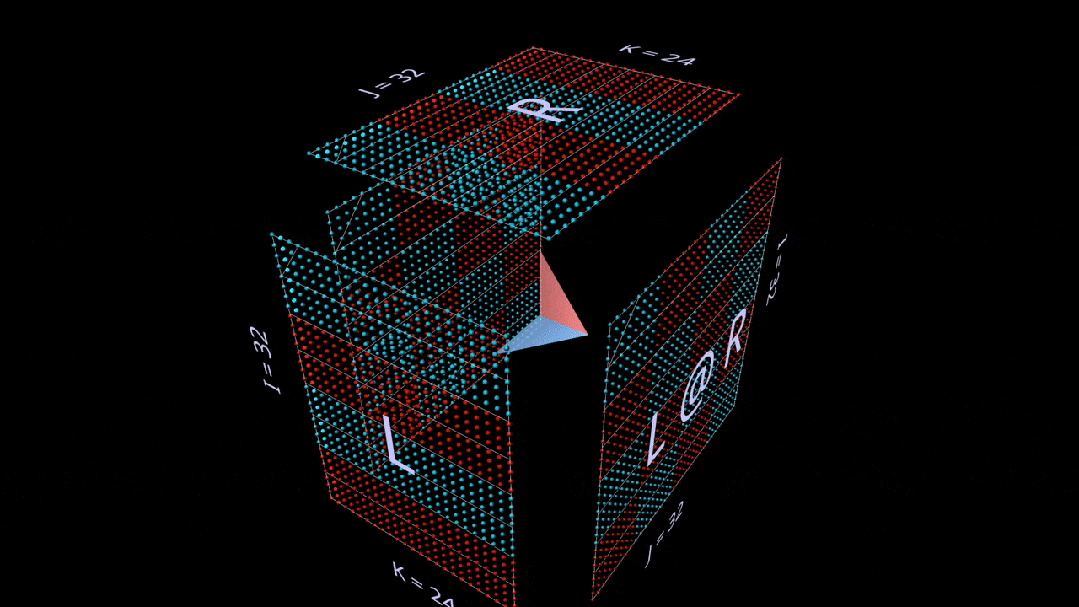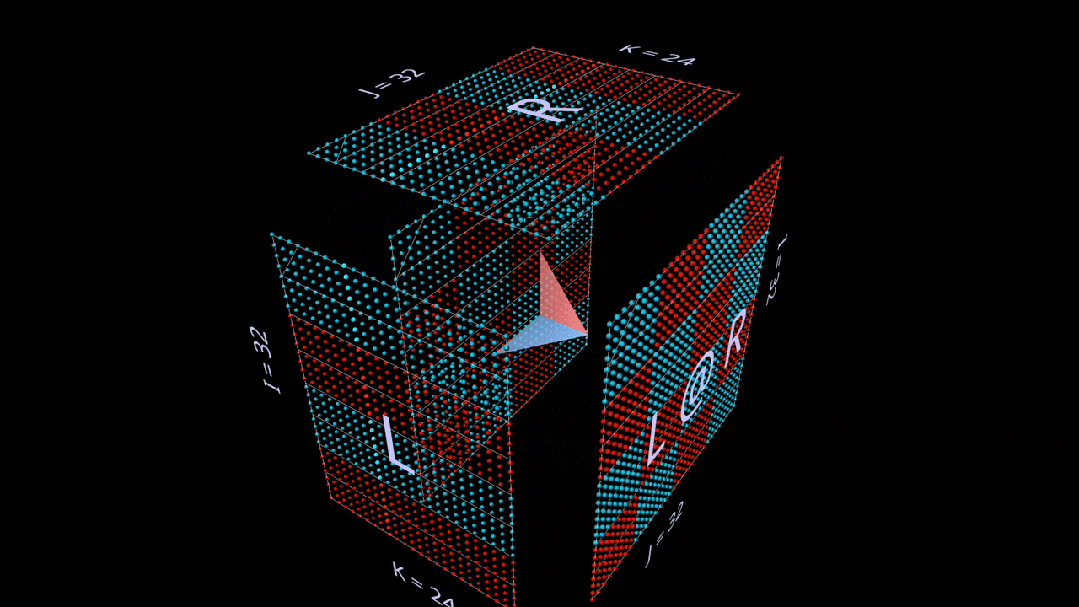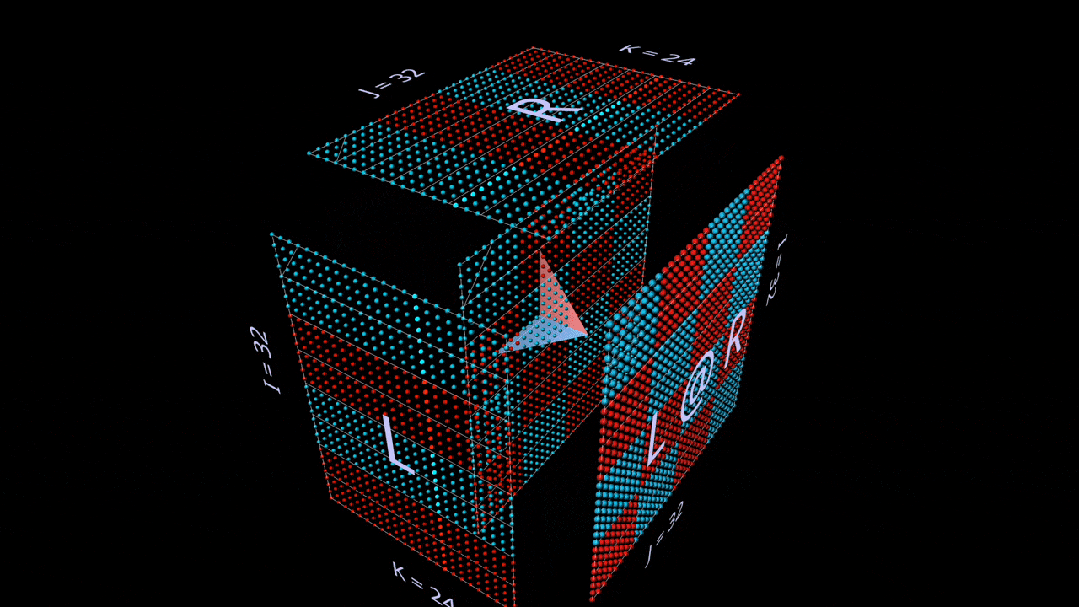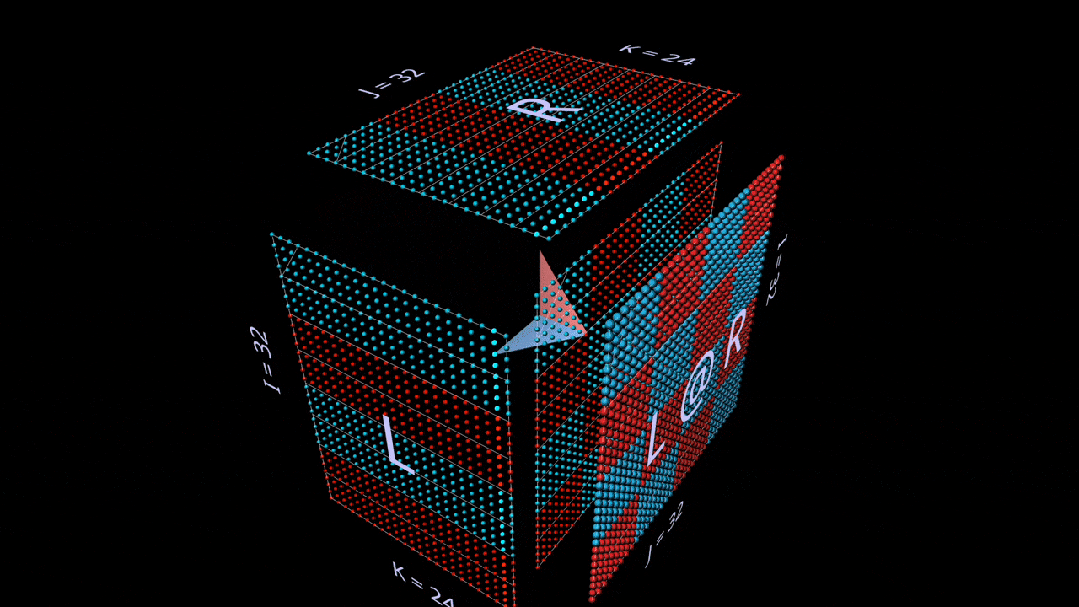
使用随机初始化的矩阵进行这种分解，我们可以看到，随着每个秩-1 外积的增加，结果中不仅有数值，还有秩的累积。

除其他外，这也让我们明白了为什么「低秩因式分解」，即通过构建深度维度参数很小的矩阵乘法来逼近矩阵，在被逼近的矩阵是低秩矩阵时效果最好。

LoRA 将在后面介绍：

表达式

如何将这种可视化方法扩展到矩阵乘法的组合？

到目前为止，示例可视化了某个矩阵 L 和 R 的单一矩阵 L @ R ，如果 L 和/或 R 本身就是矩阵，并以此类推呢？

事实证明，我们可以很好地将该方法扩展到复合表达式。

关键规则很简单：子表达式（子）矩阵乘法是另一个立方体，受与父表达式相同的布局约束，子表达式的结果面同时是父表达式的相应参数面，就像共价键共享的电子一样。

在这些限制条件下，我们可以随意排列子matmul的面。

在这里，研究人员使用了工具的默认方案，即交替生成凸面和凹面的立方体，这种布局在实践中非常有效，可以最大限度地利用空间并减少遮挡。

在本节中，Pytorch将对ML模型中的一些关键构件进行可视化处理，以熟练掌握可视化习惯用语，并了解即使是简单的示例也能给我们带来哪些直观感受。

左关联表达式

先来看两个(A @ B) @ C形式的表达式，每个表达式都有自己独特的形状和特征。

首先，我们将赋予 A @ B @ C以FFN的特征形状，其中「隐藏维度」比「输入」或「输出」维度更宽。(在本例中，这意味着B的宽度大于A或C的宽度）。

与单个matmul例子一样，浮动箭头指向结果矩阵，蓝色来自左参数，红色来自右参数：

接下来，将可视化 A @ B @ C ， B的宽度比A或C窄，使其呈现一个瓶颈或「自动编码器」形状：

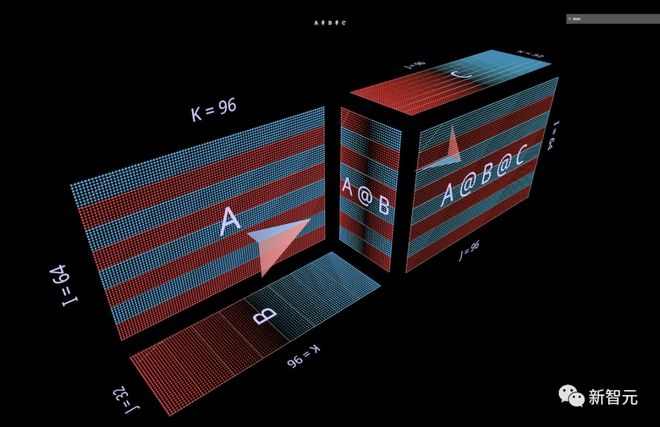
这种凸块和凹块交替出现的模式可以扩展到任意长度的链：例如这个多层瓶颈：

右关联表达式

接下来，将可视化一个右关联表达式A @ (B @ C) 。

有时，我们会看到 MLP 采用右侧关联方式，即输入层在右侧，权重层从右至左。

使用上图中的双层FFN例子中的矩阵--经过适当换位--如下所示，C现在扮演输入的角色，B是第一层，A是第二层：

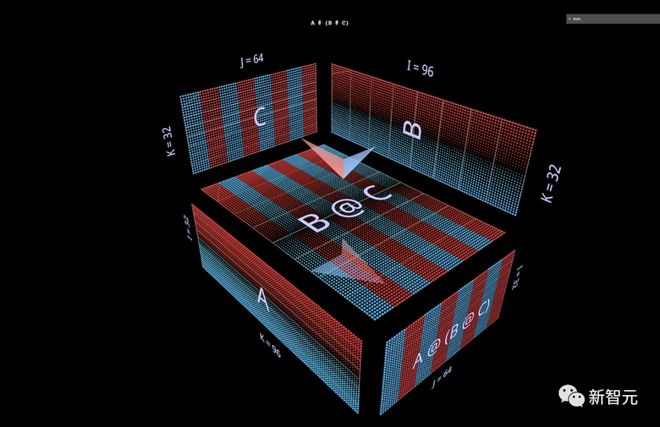
二进制表达式

可视化工具要想超越简单的教学示例之外发挥作用，就必须在表达式变得越来越复杂时，保持可读性。

在现实世界的使用案例中，二进制表达式是一个关键的结构组件，即左右两边都有子表达式的矩阵。

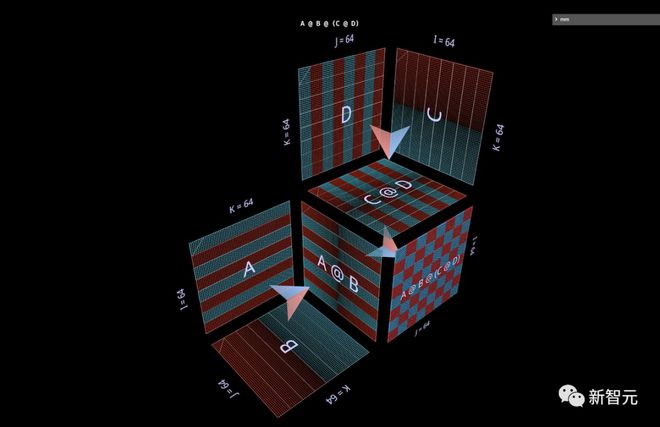
在这里，将可视化最简单的表达式形状，(A @ B) @ (C @ D) ：

分割和并行性

下面，可以通过两个快速示例来了解这种可视化风格是如何通过简单的几何分割，使复合表达式的并行化推理变得非常直观的。

在第一个例子中，把规范的「数据并行」分割应用到，上述左关联多层瓶颈的例子中。

沿着i进行分割，分割左初始参数（批）和所有中间结果（激活），但不分割后续参数（权重）。

通过几何图形，我们可以清楚地看到表达式中哪些参与者被分割，哪些参与者保持完整：

第二个例子，展示了如何通过沿着其 j 轴划分左子表达式、沿着其 i 轴划分右子表达式以及沿着其 k 轴划分父表达式来并行化二进制表达式：

注意力头内部

让我们看一个GPT2注意力头——特别是来自NanoGPT的「gpt2」（小）配置（层=12，头=12，嵌入=768）的第5层，通过HuggingFace使用OpenAI权重。

输入激活来自256个token的OpenWebText训练样本的前向传递。

研究人员之所以选择它，主要是因为它计算了一种相当常见的注意力模式，而且位于模型的中间位置，这里的激活已经变得结构化，并显示出一些有趣的纹理。

结构

整个注意力头被可视化为一个单一的复合表达式，以输入开始，以投影输出结束。(注：为了保持自成一体，研究人员按照Megatron-LM中的描述对每个头进行输出投影）。

计算包含六个矩阵：

Q = input @ wQ // 1K_t = wK_t @ input_t // 2V = input @ wV // 3attn = sdpa(Q @ K_t) // 4head_out = attn @ V // 5out = head_out @ wO // 6

我们正在查看的内容的缩略图描述：

箭头叶片是矩阵乘法1、2、3和6：前一组是从输入到 Q、K 和 V 的内投影；后一组是从 attn @ V 回到嵌入维度的外投影。

在中心是双矩阵乘法，它首先计算注意力分数（后面的凸立方体），然后使用它们从值向量（前面的凹立方体）生成输出token。因果关系意味着注意力分数形成一个下三角。

计算和值

这是一个计算注意力的动画。具体来说：

sdpa(input @ wQ @ K_t) @ V @ wO

(即上面的矩阵1、4、5 和 6，其中 K_t 和 V 是预先计算好的）的计算过程是一个融合的向量矩阵乘积链：序列中的每个项目都是一步完成，从输入到注意力再到输出的整个过程。

头的不同之处

继续下一步之前，这里还有一个演示，可以让我们简单地了解一下模型的详细工作原理。

这是GPT2的另一个注意头。

它的行为与上面的第5层第4个头截然不同，正如所预料的那样，因为它位于模型的一个非常不同的部分。

这个磁头位于第一层：第0层，头2：

并行注意力

我们将注意力头中的 6个矩阵中的4个可视化为融合的向量矩阵乘积链。

是一个融合了向量-矩阵乘积的链条，证实了从输入到输出的整个左关联链条沿着共享的 i 轴是层状的这一几何直觉，并且可以并行化。

比如沿着i分割

双分区

LoRA

最近的LoRA论文描述了一种高效的微调技术，该技术基于微调期间引入的权重增量是低秩的想法。

根据该论文，这使我们能够通过优化密集层在适应过程中变化的秩分解矩阵，间接训练神经网络中的一些密集层，同时保持预先训练的权重冻结。

基本思想

简而言之，关键的一步是训练权重矩阵的因子，而不是矩阵本身：用 I x K 张量和 K x J 张量的matmul替换 I x J 权重张量，保持 K 为某个小数字。

如果 K 足够小，那么所节省的大小将非常可观，但代价是降低 K 会降低乘积所能表达的秩。

下面是一个随机左 128 x 4 和右 4 x 128 参数的 matmul，也就是 128 x 128 矩阵的秩-4因式分解，可以快速说明节省的大小和对结果的结构影响。请注意 L @ R 的垂直和水平模式（：

参考资料：

https://twitter.com/PyTorch/status/1706384907377770884

https://twitter.com/DrJimFan/status/1706690238083744218